LeetCode 51. N 皇后
作者:Choi Yang
更新于:6 个月前
字数统计:1.1k 字
阅读时长:5 分钟
阅读量:
题目描述
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
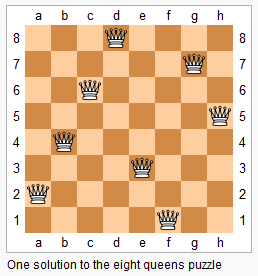
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
javascript
输入:4
输出:[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。提示:
javascript
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/n-queens 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
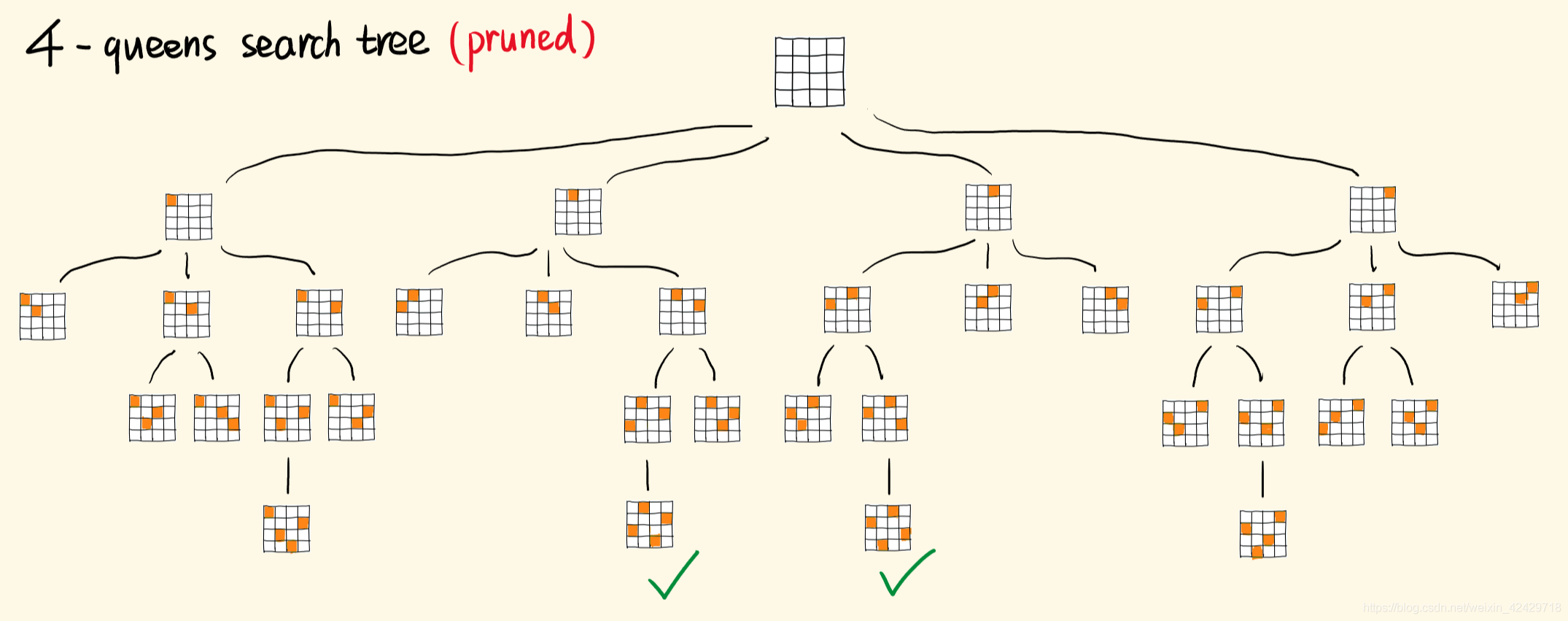
对于 n 皇后问题,经典的回溯算法,我们采用一行放一个,然后逐行来放,这样我们就不用在剪枝的时候判断是否同行了。只需要判断是否同列 或者 同一斜线就好了。
javascript
var solveNQueens = function (n) {
let res = [];
let grid = new Array(n); // 初始化一个地图
for (let i = 0; i < n; i++) {
grid[i] = new Array(n).fill(".");
}
// 剪枝条件
let check = (x, y) => {
for (let i = 0; i < x; i++) {
for (let j = 0; j < n; j++) {
// 判断同列 或者 同一斜线即可(不需要判断同行是因为一行一行放的,一定不同行)
if (grid[i][j] == "Q" && (j == y || i + j == x + y || i - j == x - y)) {
return true;
}
}
}
return false;
};
let dfs = (t) => {
if (t === n) {
let ans = grid.slice(); // 拷贝一份,对输出做处理
for (let i = 0; i < n; i++) {
ans[i] = ans[i].join("");
}
res.push(ans);
return;
}
for (let i = 0; i < n; i++) {
if (check(t, i)) continue;
grid[t][i] = "Q";
dfs(t + 1);
grid[t][i] = ".";
}
};
dfs(0);
return res;
};cpp
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> res;
vector<string> board(n, string(n, '.'));
backtrack(res, board, 0);
return res;
}
void backtrack(vector<vector<string>>& res, vector<string>& board, int row) {
if (row == board.size()) {
res.push_back(board);
return;
}
int n = board[row].size();
for (int col = 0; col < n; col++) {
if (!isValid(board, row, col)) continue;
board[row][col] = 'Q';
backtrack(res, board, row + 1);
board[row][col] = '.';
}
}
bool isValid(vector<string>& board, int row, int col) {
int n = board.size();
// 检查列是否有皇后互相冲突
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q') return false;
}
// 检查右上方是否有皇后互相冲突
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q') return false;
}
// 检查左上方是否有皇后互相冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') return false;
}
return true;
}
};java
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> res = new ArrayList<>();
char[][] board = new char[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(board[i], '.');
}
backtrack(res, board, 0);
return res;
}
private void backtrack(List<List<String>> res, char[][] board, int row) {
if (row == board.length) {
res.add(charToString(board));
return;
}
int n = board[row].length;
for (int col = 0; col < n; col++) {
if (!isValid(board, row, col)) continue;
board[row][col] = 'Q';
backtrack(res, board, row + 1);
board[row][col] = '.';
}
}
private boolean isValid(char[][] board, int row, int col) {
int n = board.length;
// 检查列是否有皇后互相冲突
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q') return false;
}
// 检查右上方是否有皇后互相冲突
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q') return false;
}
// 检查左上方是否有皇后互相冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') return false;
}
return true;
}
private List<String> charToString(char[][] board) {
List<String> res = new ArrayList<>();
for (char[] chars : board) {
res.add(new String(chars));
}
return res;
}
}python
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
res = []
board = [['.'] * n for _ in range(n)]
def backtrack(board, row):
if row == len(board):
res.append([''.join(row) for row in board])
return
n = len(board[row])
for col in range(n):
if not isValid(board, row, col):
continue
board[row][col] = 'Q'
backtrack(board, row + 1)
board[row][col] = '.'
def isValid(board, row, col):
n = len(board)
# 检查列是否有皇后互相冲突
for i in range(n):
if board[i][col] == 'Q':
return False
# 检查右上方是否有皇后互相冲突
i, j = row - 1, col + 1
while i >= 0 and j < n:
if board[i][j] == 'Q':
return False
i, j = i - 1, j + 1
# 检查左上方是否有皇后互相冲突
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if board[i][j] == 'Q':
return False
i, j = i - 1, j - 1
return True
backtrack(board, 0)
return resjavascript
学如逆水行舟,不进则退