LeetCode 212. 单词搜索 II

作者:Choi Yang

更新于:6 个月前

字数统计:2k 字

阅读时长:9 分钟

阅读量:

题目描述

给定一个二维网格 board 和一个字典中的单词列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例:

javascript

输入:
words = ["oath","pea","eat","rain"] and board =
[
  ['o','a','a','n'],
  ['e','t','a','e'],
  ['i','h','k','r'],
  ['i','f','l','v']
]

输出: ["eat","oath"]
说明:
你可以假设所有输入都由小写字母 a-z 组成。

提示:

javascript

你需要优化回溯算法以通过更大数据量的测试。你能否早点停止回溯？
如果当前单词不存在于所有单词的前缀中，则可以立即停止回溯。什么样的数据结构可以有效地执行这样的操作？散列表是否可行？为什么？ 前缀树如何？如果你想学习如何实现一个基本的前缀树，请先查看这个问题： 实现Trie（前缀树）。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/word-search-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

参考力扣官网分析：实现 Trie (前缀树)

https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/

chodocs.cn

判断是否找到了，通过传递节点的 END 来判断
判断是否重复访问，通过动态更改走过的网格点来判断，就不需要再定义一个vis数组了

参考大佬：秦时明月字典树建树解法（二）

https://leetcode-cn.com/problems/word-search-ii/solution/212-dan-ci-sou-suo-ii-by-alexer-660/

chodocs.cn

javascriptcppjavapython

javascript

var findWords = function (grid, words) {
  // 存放最终结果集
  let res = [];
  // 字典树节点
  class TrieNode {
    constructor() {
      this.end = false;
      this.child = {};
    }
  }
  // 最终形成的字典树根节点
  let root = null;
  let Trie = function () {
    root = new TrieNode();
  };
  // 建立字典树
  Trie.prototype.insert = (word) => {
    let cur = root;
    for (let i = 0; i < word.length; i++) {
      if (!cur.child[word[i]]) {
        cur.child[word[i]] = new TrieNode();
      }
      cur = cur.child[word[i]];
    }
    cur.end = true;
  };
  // 创建根节点
  let trie = new Trie();
  // 进行建树操作
  for (let i = 0; i < words.length; i++) {
    trie.insert(words[i]);
  }
  let dfs = (x, y, t, cur) => {
    if (cur.end) {
      res.push(t);
      cur.end = false; // 避免重复计算
    }
    // 剪枝条件：1.边界处理 2.下一步是否可走 3.下一步字典树是否可走
    if (
      x < 0 ||
      x >= grid.length ||
      y < 0 ||
      y >= grid[0].length ||
      grid[x][y] == "#" ||
      !cur.child[grid[x][y]]
    )
      return;
    let tmp = grid[x][y];
    grid[x][y] = "#"; // 走
    cur = cur.child[tmp];
    dfs(x + 1, y, t + tmp, cur); // 上下左右四个方向遍历
    dfs(x, y + 1, t + tmp, cur);
    dfs(x - 1, y, t + tmp, cur);
    dfs(x, y - 1, t + tmp, cur);
    grid[x][y] = tmp; // 回溯（还原）
  };
  // 对单词表进行全局搜索
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      dfs(i, j, "", root);
    }
  }
  return res;
};

cpp

class TrieNode {
public:
    TrieNode* child[26];
    string str;
    TrieNode() {
        for (auto &a : child) a = NULL;
    }
};

class Solution {
public:
    vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
        vector<string> res;
        TrieNode* root = buildTrie(words);
        for (int i = 0; i < board.size(); ++i) {
            for (int j = 0; j < board[0].size(); ++j) {
                dfs(board, i, j, root, res);
            }
        }
        return res;
    }
    TrieNode* buildTrie(vector<string>& words) {
        TrieNode* root = new TrieNode();
        for (auto &a : words) {
            TrieNode* t = root;
            for (auto &c : a) {
                int i = c - 'a';
                if (!t->child[i]) t->child[i] = new TrieNode();
                t = t->child[i];
            }
            t->str = a;
        }
        return root;
    }
    void dfs(vector<vector<char>>& board, int i, int j, TrieNode* p, vector<string>& res) {
        char c = board[i][j];
        if (c == '#' || !p->child[c - 'a']) return;
        p = p->child[c - 'a'];
        if (p->str.size() > 0) {
            res.push_back(p->str);
            p->str = "";
        }

        board[i][j] = '#';
        if (i > 0) dfs(board, i - 1, j ,p, res);
        if (j > 0) dfs(board, i, j - 1, p, res);
        if (i < board.size() - 1) dfs(board, i + 1, j, p, res);
        if (j < board[0].size() - 1) dfs(board, i, j + 1, p, res);
        board[i][j] = c;
    }
};

java

class Solution {
    public List<String> findWords(char[][] board, String[] words) {
        List<String> res = new ArrayList<>();
        TrieNode root = buildTrie(words);
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                dfs(board, i, j, root, res);
            }
        }
        return res;
    }

    private void dfs(char[][] board, int i, int j, TrieNode p, List<String> res) {
        char c = board[i][j];
        if (c == '#' || p.next[c - 'a'] == null) return;
        p = p.next[c - 'a'];
        if (p.word != null) {
            res.add(p.word);
            p.word = null;
        }

        board[i][j] = '#';
        if (i > 0) dfs(board, i - 1, j ,p, res);
        if (j > 0) dfs(board, i, j - 1, p, res);
        if (i < board.length - 1) dfs(board, i + 1, j, p, res);
        if (j < board[0].length - 1) dfs(board, i, j + 1, p, res);
        board[i][j] = c;
    }

    private TrieNode buildTrie(String[] words) {
        TrieNode root = new TrieNode();
        for (String w : words) {
            TrieNode p = root;
            for (char c : w.toCharArray()) {
                int i = c - 'a';
                if (p.next[i] == null) p.next[i] = new TrieNode();
                p = p.next[i];
            }
            p.word = w;
        }
        return root;
    }

    class TrieNode {
        TrieNode[] next = new TrieNode[26];
        String word;
    }
}

python

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        if not board or not board[0]: return []
        if not words: return []
        self.res = set()
        root = {}
        for word in words:
            node = root
            for char in word:
                node = node.setdefault(char, {})
            node['#'] = '#'
        self.m, self.n = len(board), len(board[0])
        self.board = board
        for i in range(self.m):
            for j in range(self.n):
                if board[i][j] in root:
                    self.dfs(i, j, '', root)
        return list(self.res)

    def dfs(self, i, j, cur_word, cur_dict):
        cur_word += self.board[i][j]
        cur_dict = cur_dict[self.board[i][j]]
        if '#' in cur_dict:
            self.res.add(cur_word)
        tmp, self.board[i][j] = self.board[i][j], '@'
        for dx, dy in [[-1, 0], [1, 0], [0, -1], [0, 1]]:
            x, y = i + dx, j + dy
            if 0 <= x < self.m and 0 <= y < self.n and self.board[x][y] != '@' and self.board[x][y] in cur_dict:
                self.dfs(x, y, cur_word, cur_dict)
        self.board[i][j] = tmp

附上完整字典树（前缀树）模板，日后可用~

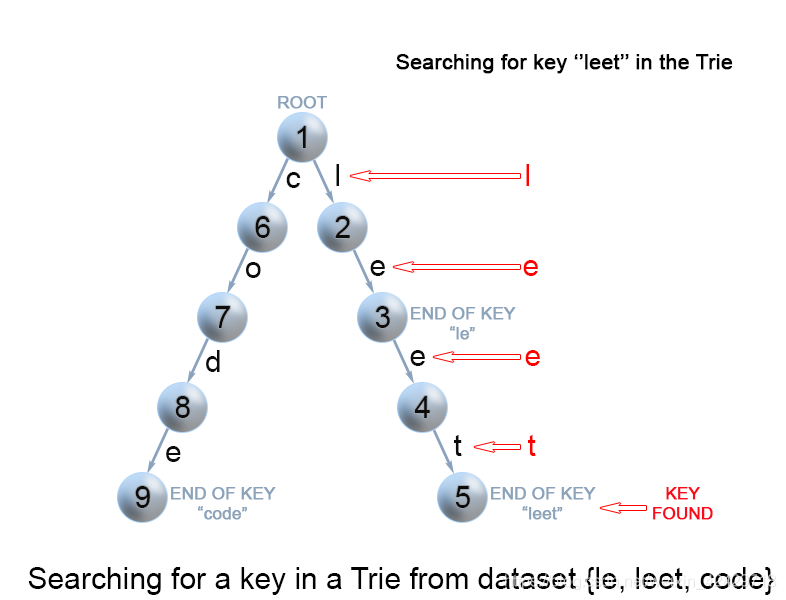
在 Trie 树中查找键

每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始，。检查当前节点中与键字符对应的链接。有两种情况：

存在链接。我们移动到该链接后面路径中的下一个节点，并继续搜索下一个键字符。
不存在链接。若已无键字符，且当前结点标记为 isEnd，则返回 true。否则有两种可能，均返回 false : 还有键字符剩余，但无法跟随 Trie 树的键路径，找不到键。没有键字符剩余，但当前结点没有标记为 isEnd。也就是说，待查找键只是Trie树中另一个键的前缀。

查找 Trie 树中的键前缀

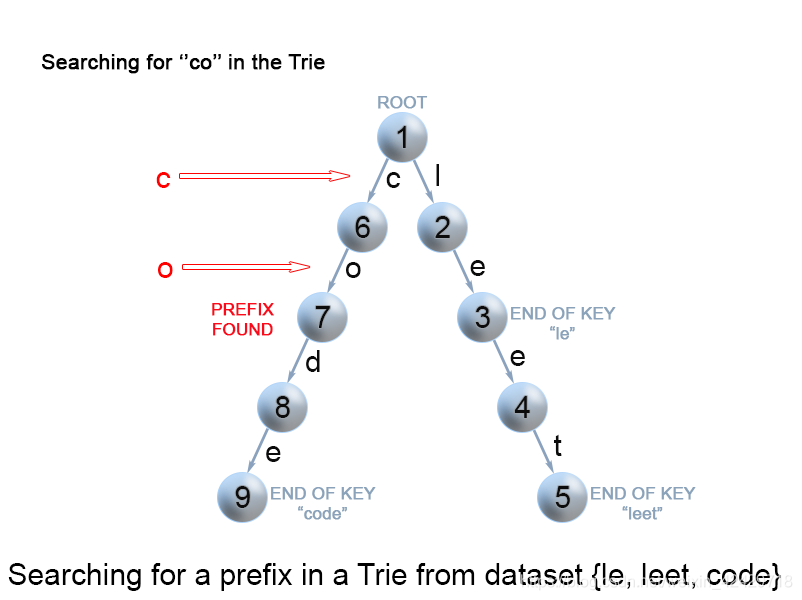
该方法与在 Trie 树中搜索键时使用的方法非常相似。我们从根遍历 Trie 树，直到键前缀中没有字符，或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是，到达键前缀的末尾时，总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记，因为我们搜索的是键的前缀，而不是整个键。

作者：LeetCode 链接：https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/ 来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

javascript

var findWords = function (grid, words) {
  // 存放最终结果集
  let res = [];
  // 字典树节点
  class TrieNode {
    constructor() {
      this.end = false;
      this.child = {};
    }
  }
  // 最终形成的字典树根节点
  let root = null;
  let Trie = function () {
    root = new TrieNode();
  };
  // 建立字典树
  Trie.prototype.insert = (word) => {
    let cur = root;
    for (let i = 0; i < word.length; i++) {
      if (!cur.child[word[i]]) {
        cur.child[word[i]] = new TrieNode();
      }
      cur = cur.child[word[i]];
    }
    cur.end = true;
  };
  // 在 Trie 树中查找键
  let searchPrefix = (word) => {
    let cur = root;
    for (let i = 0; i < word.length; i++) {
      if (cur.child[word[i]]) {
        cur = cur.child[word[i]];
      } else {
        return null;
      }
    }
    return cur;
  };
  Trie.prototype.search = (word) => {
    let cur = searchPrefix(word);
    return cur !== null && cur.end;
  };
  // 查找 Trie 树中的键前缀
  Trie.prototype.startsWith = (pre) => {
    return searchPrefix(pre) != null;
  };
  // 创建根节点
  let trie = new Trie();
  // 进行建树操作
  for (let i = 0; i < words.length; i++) {
    trie.insert(words[i]);
  }
  let dfs = (x, y, t, cur) => {
    if (cur.end) {
      res.push(t);
      cur.end = false; // 避免重复计算
    }
    // 剪枝条件：1.边界处理 2.下一步是否可走 3.下一步字典树是否可走
    if (
      x < 0 ||
      x >= grid.length ||
      y < 0 ||
      y >= grid[0].length ||
      grid[x][y] == "#" ||
      !cur.child[grid[x][y]]
    )
      return;
    let tmp = grid[x][y];
    grid[x][y] = "#"; // 走
    cur = cur.child[tmp];
    dfs(x + 1, y, t + tmp, cur); // 上下左右四个方向遍历
    dfs(x, y + 1, t + tmp, cur);
    dfs(x - 1, y, t + tmp, cur);
    dfs(x, y - 1, t + tmp, cur);
    grid[x][y] = tmp; // 回溯（还原）
  };
  // 对单词表进行全局搜索
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      dfs(i, j, "", root);
    }
  }
  return res;
};

javascript

学如逆水行舟，不进则退

Contributors

Choi Yang

LeetCode 212. 单词搜索 II ​

题目描述 ​

解题思路 ​

Contributors ​

LeetCode 212. 单词搜索 II

题目描述

解题思路

Contributors